

This purpose of this assignment was to reduce a specified set of range data by replacing dense sets of points with geometry.
This assignment consisted of 5 steps:
The data we were given consisted of 1,101,600 (x, y, z) locations for samples collected through 6 range scans of a room. Since much of the data in the 6 scans overlapped, a student in our class, Justin Talbot, was able to use a free software package from Stanford University to help figure out the transformation matrices for the of the 6 data sets. I multiply each of the data points by their transformation as they are read into my program. There are a significant number of points that appear to make a large ring or dome around the data. I consider these points outliers and drop them from the data set if the absolute value of either of their x, y or z values is greater than 1000.0.
Once all the data is read in, I use a virtual grid to reduce its size. The (x, y, z) location of each grid point is the average of all the points that fall within that cell. The reason I use a virtual grid is that I want to be able to have a large resolution on the grid, say 1000X1000X1000 or more. This would require an incredible amount of memory (1,000,000,000 cells) to store all of the cells, and most of them would remain unused. So I implement a hash table to act as the virtual grid. The size of the hash table I use is 2000. I used the unique grid ID for each cell to act as the hash key. The grid ID for each cell is given by:
I pick a resolution for the grid by means of a scale factor (0.15). Every point is multiplied by this scale factor and the fractional parts of the resulting value were dropped to give each point an x,y,z location in the virtual grid. I picked the resolution value based on looking at the data and deciding if there were enough remaining points to adequately represent the data.
I use several methods to fit planes to the data. This is the most complex and time consuming part of the process and is divided into several categories below.
I decided to take a computer vision approach to this problem by using a Hough transform for points and planes. I devised my own, but the derivation seems straight forward for given the problem. In my implementation, I first create a hemisphere of N*(N-1) normals where N is the number of evenly spaced samples of each of the two angles. One thing to note is that the distribution of the normals is not even across the hemisphere, but I believe that N=8 gives me a sufficient variety of possible planes for the data set. If it is insufficient, it may easily be increased. The reason I use just less than a hemisphere of normals is to avoid duplicating r values for a point.
Each Hough cell has a list of the grid points that pertain to it and an average r value for those grid points. The Hough cells are implemented as a 2D array whose first index is the id of the plane normal. The second dimension of the array tells how many Hough cells there may be in any of the 56 directions. I use 128 in my implementation.
For every grid point, I calculate an offset r for the 56 different plane normals. This gives me an equation for 56 different planes that pass through the grid point. I then add this Hough cell to my 2D Hough array. If there is already a Hough cell with the same normal and close to the same r, I add the grid point to that existing Hough and average in the r value. —I use I use 1.0/0.075 = 13.3 as my tolerance for r based on visual results with one of the data sets.
I define “cleaning the Hough” to mean merging dividing and pruning the Hough planes so that they are more representative of the data. After the Hough array has been created, I then proceed to clean it up by first merging Hough cells that have r values within 13.3. This is done because after adding multiple grid points to the Hough cells, some of the adjusted r values will be very close to each other. While merging similar Hough cells, I also invalidate cells that contain less than 10 grid points.
Once the Hough cells are merged, I break down each Hough cell based on connected components of its grid points and once again invalidate any small cells. I use a recursive algorithm to create connected components, and it ends up being the most time intensive part of the program. I set the tolerance on distance in connected components to be 2.0/grid_scale_factor. This allows for a little bit of noise in the data.
Once again I pass through all the Hough planes and invalidate any planes that have less than 20 grid points. This is twice the previous tolerance for valid Hough planes.
The final step of my clean up is to invalidate any planes that have a compactness of less than 0.5. I calculate the compactness of a Hough plane by projecting its grid points onto a discrete 2D grid that is the best fit bounding box on the grid points in the plane. I then count the number of marked grid positions and divide it my the total size of the grid. I choose the resolution of the grid by multiplying the width and height of the bounding box of the plane by half the grid_scale_factor. To find the tightest bounding box, I use 4 unique evenly spaced box orientations.
After the Hough cells have been cleaned up, I go through every grid point and find the best Hough cell for that particular point. In my implementation, I choose the Hough cell that has the greatest number of points in it that also contains the grid point in question. This Hough cell is then added to a new set of planes. If a plane exists for a given Hough cell, then the grid point is added to that plane. This way each grid point ends up belonging to at most one plane. Because of clean up, some grid points will not have a valid Hough plane. This is okay so long as we get enough planes to represent the data. The final step in picking the planes is to remove any planes that have less than 10 grid points.
For simplicity, I represent each of the final planes by a minimal bounding box on the grid points in the plane. This box is calculated in the same fashion as when I calculate compactness. The bounding box in 3D is just the inverse transformation of the projected plane.
In my results, there are still a few planes that overlap each other. This can be eliminated by performing a connected component operation on the planes as was done during the Hough clean up phase.
I use OpenGL to render the points and quadrilaterals. I render the quads with 50% alpha so that the viewer can see through the data. Rendering the quads in solid color and using lighting would also be helpful when viewing the planes. I save the geometry to a file that may be read into another program for viewing
Here are some views of the rendered data and planes
Largest initial plane in a one of the six room data sets.

One of the six room data sets. Points colored by plane.

Planar fit of one of the six room data sets.
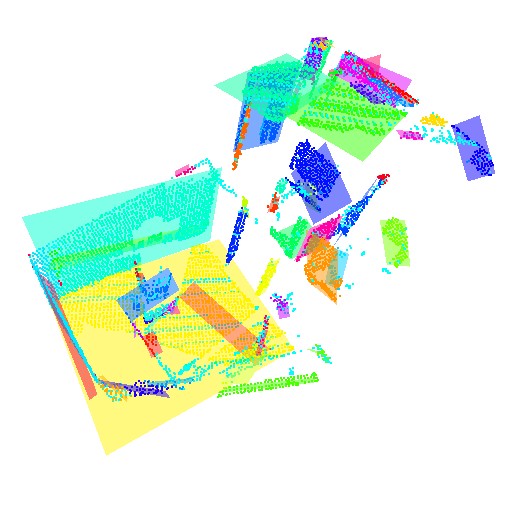
Planar fit of one the entire room data set.
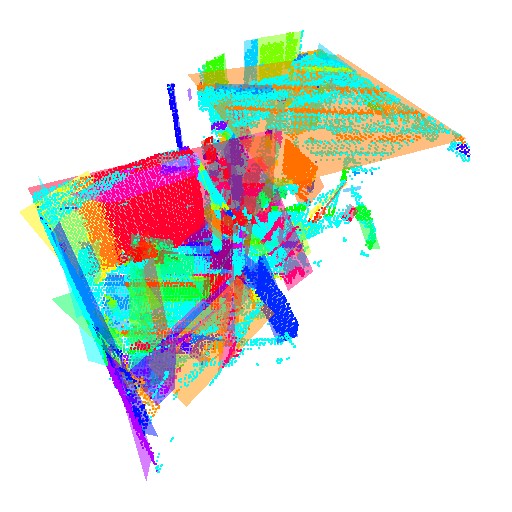

I tested the robustness of my algorithm on the Stanford bunny, acquired from Stanford's computer graphics web site. The algorithm did not give very good results. I believe this is because I had set the tolerances for the virtual grid and the Hough planes to work well for the room data set. I do believe that tweaking the values will allow the Stanford bunny to be better represented by my algorithm.



I was very happy with the results of my algorithm on the Room. I was able to identify the floor, walls, ceiling, table, and pillars in the scene.
There are several things I think I could do to improve my results on the Stanford bunny and other similar data sets. The main improvement would be to automatically set the virtual grid and Hough plane resolution based on the size of the data and the number of points in each direction. Doing a connected components on the resulting planes would also help eliminate overlapping planes in the final data set.
| Data Set | Number of Original Points | Number of Extracted Quads | Reduction in Points |
| Room | 1,101,600 | 136 | 99.95% |
| Stanford Bunny | 35,947 | 32 | 99.64% |
Right click on the links below to download the code and some sample data.
One of the six data sets used for the room (*.zip) [1.7 MB]
Code for the generating and viewing planar fits of data (*.zip) [13 KB]